Teorema
Frisch Waugh Lovell
Considere el modelo $ Y = X_{1}\beta_{1} + X_{2}\beta_{2} +\epsilon $ donde $ X_{1} $ y $ X_{2} $ pueden ser matrices o vectores. Según el teorema de Frisch Waugh, el vector de coeficientes $ \beta_{1} $ puede estimarse corriendo los residuos de una regresión de Y contra todas las variables de $ X_{2} $ , contra los residuos de una regresión de cada variable $ X_{1} $ contra todas las variables de $ X_{2} $ . Este procedimiento arroja $ \hat{\beta} $ y $ \hat{\epsilon} $ correctos. También se puede correr $ Y $ directamente contra los residuos de una regresión de cada variable $ X_{1} $ contra todas las variables de $ X_{2} $ ; en este caso, la estimación para $ \beta_{1} $ será correcta pero no los residuos ε gorro. Igual para $ \beta_{2} $1.
Veamoslo en Stata:
Primero debemos crear nuestras variable asegurandonos que exista una correlacion entre $ X_{1} $ y $ X_{2} $.
clear
set seed 21008
set obs 1000
gen x1 = rnormal()
gen x2 = rnormal() + 0.2*x1

Proceso generador de datos para y.
gen y = 4 + x1 + 5*x2 + rnormal()
Ahora hay que realizar la regresion de $ y $ en $ x_{2} $ y de $ x_{1} $ en $ x_{2} $ para luego obtener los residuos.
reg x1 x2
predict resid_x1, res
reg y x2
predict resid_y, res
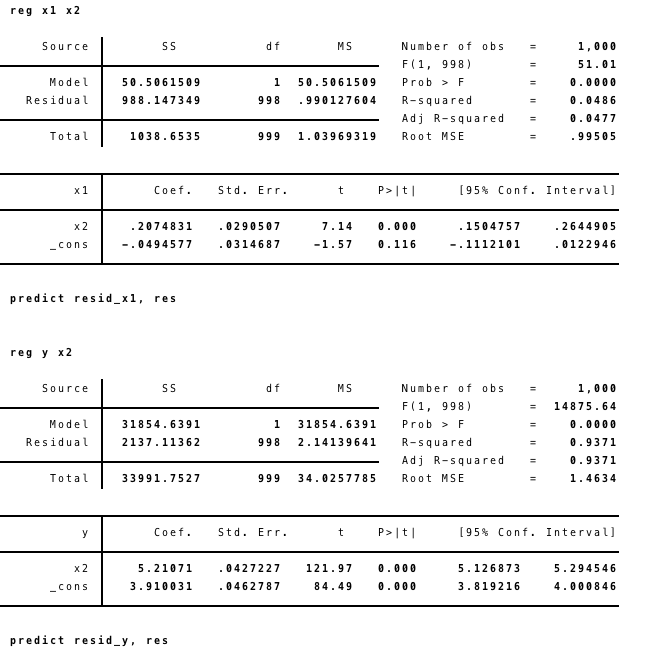
Por ultimo realizaremos la regresion de los residuos obtenidos anteriormente y la regresion usual por MCO para comprobar si nuestro estimador $ \beta_{1} $ es igual.
reg resid_y resid_x1
outreg2 using myreg.doc, replace ctitle(Modelo FWL)
reg y x1 x2
outreg2 using myreg.doc, append ctitle(Modelo Correcto)
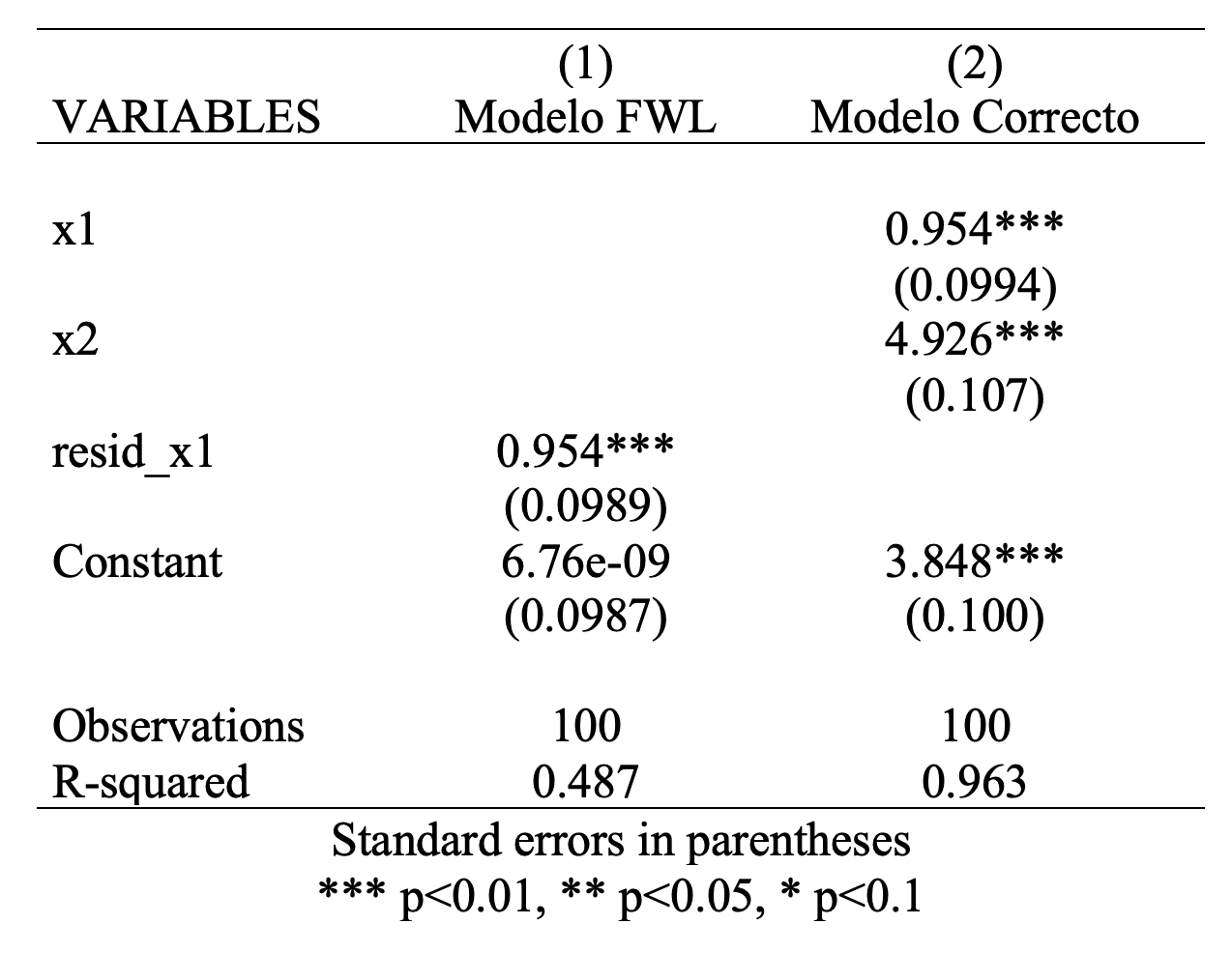
En conclusion gracias al teorema FWL el coeficiente que obtenemos para un modelo de regresion múltiple es igual al coeficiente del modelo de regresión simple si se "elimina" la influencia de los otros regresores.
Bibliografía:
- Verbeek, M. (2004), A Guide to Modern Econometrics.
- Wooldridge, Jeffrey M. (2018), Introductory Econometrics: A Modern Approach, Sixth Edition, Cengage Learning.
- Montenegro, A. (2018), Econometría Intermedia y Básica.