Simulaciones
de Montecarlo

El método de Monte Carlo, consiste en realizar y tabular muchísimas repeticiones de un experimento construyendo nuestras variables en cada repetición tomando un generador de números aleatorios1.Con esta herramienta demostrarémos insesgamiento y consistencia.

Insesgamiento

Decimos que nuestros estimadores son insesguados cuando en un muestreo repetido nuestro estimador es en promedio igual al valor real del parametro poblacional2. Matematicament diremos que $E {\hat{\beta}} = \beta $. En otras palabras "en promedio, un estimador insesgado da en el blanco."1

Matematicamente:

$$ \hat{\beta} = (X'X)^{-1}X'y $$ $$ \hat{\beta} = (X'X)^{-1}X'(X\beta + \epsilon) $$ $$ \hat{\beta} = (X'X)^{-1}X'X\beta + (X'X)^{-1}X'\epsilon $$ $$ \hat{\beta} = \beta + (X'X)^{-1}X'\epsilon\ $$

Tomando valor esperado

$$ E\hat{\beta} = \beta + E[(X'X)^{-1}X'\epsilon] $$

Viendo lo anterior vemos que para que nuestro estimador sea insesgado necesitaremos que el termino $ E[(X'X)^{-1}X'\epsilon] $ sea igual a 0. Esto ocurre cuando se cumple el supuesto de Gauss Marvok de exogeneidad estricta, es decir, necesitamos que el valor esperado del vector $ \epsilon $ condicionado la matriz X sea 0.

Veamos como se vería esto en Stata:


clear
set obs 1000
gen B1_store=.

set obs 10000
gen poblacionx=runiform(0,5)
gen epsilon=rnormal(0,1)
gen poblaciony=0.8*poblacionx+epsilon

						

qui forvalues i =1/1000{
gen random= runiform()
sort random
mata: ym = st_data((1,1000), "poblaciony")
mata: xm = st_data((1,1000), "poblacionx")
mata betaest = invsym(xm'xm)*xm'ym
mata: betaest
mata: st_numscalar("beta_1" , betaest)
local coef1= beta_1
replace B1_store= `coef1'  in `i'
drop random
}



summ 	B1_store

Como podemos ver despues de realizar 1000 simulaciones obtenemos que la media de todas estas estimaciones es 0.803, un valor bastante cercano al valor poblacional (0.8). Este valor se acercara cada vez mas al poblacional a medida que aumentamos la muestra. 



histogram B1_store, percent fcolor(none) lcolor(ebblue*.7) ytitle(Densidad) xtitle(Betas) xline(0.8, lwidth(thick) lpattern(dash) lcolor(orange*1)) title(Distribución Muestral 1000 Repeticiones)

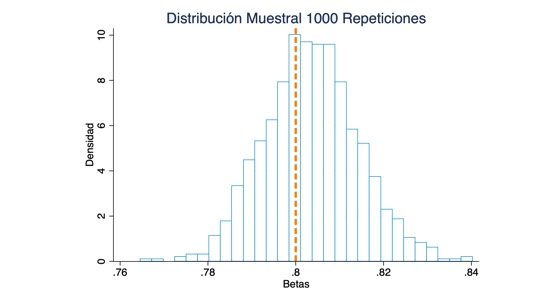
En el histograma es mas claro que el valor esperado del estimador de beta de MCO es igual a su valor poblacional (insesgamiento). Como ya se menciono, para que esto ocurra necesitamos que el valor esperado del error condicionado X sea 0, es decir, necesitamos el supuesto de exogeneidad estricta. Esto lo impusimos en stata al crear un $ \epsilon $ no correlacionado con $ X $.

Consistencia

Se dice que un estimador $ \hat{\beta}$ es consistente si se cumple que $ plim(\hat{\beta}) = \beta $, donde $ \beta $ es el verdadero parámetro de la población. Hay que tener en cuenta que la mera existencia de $ plim(\hat{\beta}) $ no garantiza consistencia porque para ello dicho $ plim(\hat{\beta}) $ debe ser igual al verdadero parámetro poblacional. En otras palabras consistencia implica que conseguir más datos (ampliar la muestra) ayuda al estimador a acercarse en probabilidad al verdadero parámetro.3

Podemos empezar mostrando que bajo los supuestos de Gauss-Markov, se cuple que $ plim(\hat{\beta}) = \beta $, es decir, que el estimador es consistente.

$$\hat{\beta} = (X'X)^{-1}X'Y$$ $$\hat{\beta} = (X'X)^{-1}X'Y (\frac{n}{n})$$ $$\hat{\beta} = (\frac{X'X}{n})^{-1} (\frac{X'Y}{n})$$ $$\hat{\beta} = (\frac{X'X}{n})^{-1} (\frac{X'(X\beta + \epsilon)}{n})$$ $$\hat{\beta} = \underbrace{(\frac{X'X}{n})^{-1} (\frac{X'X}{n})}_I\beta +(\frac{X'X}{n})^{-1}(\frac{X'\epsilon}{n}) $$ $$\hat{\beta} = \beta +(\frac{X'X}{n})^{-1}(\frac{X'\epsilon}{n})$$ $$plim(\hat{\beta}) = plim\beta + plim(\frac{X'X}{n})^{-1}(\frac{X'\epsilon}{n}) $$ $$plim(\hat{\beta}) =\beta + E[X'X]^{-1} E[X'\epsilon]$$

Entonces, cuando $E[X'\epsilon] = 0$ nuestros estimadores serán consistentes,es decir cuando tenemos exogeneidad estricta y errores homocedasticos.

$$plim(\hat{\beta}) = \beta$$

Veamos como sería en Stata


clear
set obs 10000
gen N=.
gen B1_store=.
gen poblacionx=runiform(0,5)
gen epsilon=rnormal(0,1)
gen poblaciony=0.8*poblacionx+epsilon

		

qui forvalues i = 5 10 to 10000{

set obs 10000
gen random= runiform()
sort random
mata: ym = st_data((1,`i'), "poblaciony")
mata: xm = st_data((1,`i'), "poblacionx")
mata: betaest = invsym(xm'xm)*xm'ym
mata: betaest
mata st_numscalar("beta_1" , betaest)
local coef1= beta_1
replace B1_store= `coef1'  in `i'
replace N=`i' in `i'
drop random
}




twoway 	 (scatter B1_store N)

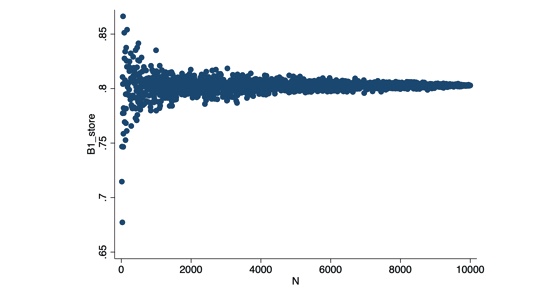
Aquí logramos ver que a medida que aumenta el tamaño de la muestra (N), nuestro estimador se acerca mas al valor 0.8 (el valor poblacional que habíamos establecido). En otras palabras, mientras se cumplan los supuestos de Gauss Markov (específicamente no colinealidad perfecta y no correlación serial), el estimador de MCO será consistente.

Bibliografía:

Bases y do files