Normalidad Asintótica

Cuando se viola el supuesto de que los errores se distribuyen normal con media 0 y varianza $σ^{2} I_{N}$ empezamos a tener problemas de inferencia estadística. ¿Por qué? Porque si no se cumple el supuesto de normalidad ya no sabemos si $\hat{β}$ se distribuye o no normal, y por ende no podemos calcular los estadísticos F o t.
Lo bueno es que hay una solución, ya que este supuesto no es necesario cuando tenemos un tamaño de muestra "n" grande. En esta sección vamos a demostrar usando Stata, que con un n grande, tendremos que: $\sqrt{n} (β - \hat{β}) \underset{D i s t r i b u c i o n}{\underset{⏟}{⟶}} N (0, A V a r (\hat{β}))$ Es decir, $\sqrt{n} (β - \hat{β})$ \textbf{converge en distribución} a $N (0, A V a r (\hat{β}))$ Para demostrar esto, partimos de nuestro estimador $\hat{β}$ y llegamos a la forma $\sqrt{n} (\hat{β} - β)$ , luego veremos a que convergen los términos restantes (Spoiler: Llegaremos a una función de la forma $A_{n} Z_{n}$ , donde $A_{n}$ es una variable aleatoria que converge en probabilidad a una constante A, y $Z_{n}$ es una variable aleatoria que converge en distribución a una normal) y para terminar, usaremos el teorema de Slutsky para ver a que converge la función restante (la cual tendrá una forma tipo $A_{n} Z_{n}$ ). Entonces, partiendo de nuestros estimadores escritos en forma matricial: $\hat{β} = (X^{'} X)^{- 1} X^{'} Y$ $\hat{β} = β + (X^{'} X)^{- 1} X^{'} ϵ$ $\hat{β} - β = (X^{'} X)^{- 1} X^{'} ϵ (\frac{n}{n})$ $\hat{β} - β = (X^{'} X)^{- 1} X^{'} ϵ (\frac{n}{\sqrt{n} \sqrt{n}})$ $\sqrt{n} (\hat{β} - β) = (X^{'} X)^{- 1} X^{'} ϵ (\frac{n}{\sqrt{n}})$ $\sqrt{n} (\hat{β} - β) = (\frac{X^{'} X}{n})^{- 1} (\frac{X^{'} ϵ}{\sqrt{n}})$ Sabemos que $(\frac{X^{'} X}{n})^{- 1}$ converge en probabilidad a $E [X^{'} X]^{- 1}$ , pero no sabemos nada sobre $(\frac{X^{'} ϵ}{\sqrt{n}})$ , asi que vamos a ver: $(\frac{X^{'} ϵ}{\sqrt{n}})$ $\underset{X}{\underset{⏟}{X^{'}}} \underset{N (0, 1)}{\underset{⏟}{(\frac{ϵ}{\sqrt{n}})}}$ Por una parte gracias al teorema del limite central, esto converge a una normal, pero no sabemos cuales serán sus momentos muéstrales. Para saberlo, tomamos valor esperado: $E [(\frac{X^{'} ϵ}{\sqrt{n}})] = 0$ Y tomamos la varianza: $V a r [(\frac{X^{'} ϵ}{\sqrt{n}})] = \frac{1}{n} X^{'} V a r (ϵ) X$ $V a r [(\frac{X^{'} ϵ}{\sqrt{n}})] = \frac{1}{n} X^{'} {σ_{ϵ}}^{2} X$ $V a r [(\frac{X^{'} ϵ}{\sqrt{n}})] = {σ_{ϵ}}^{2} \underset{E [X^{'} X]}{\underset{⏟}{(\frac{X^{'} X}{n})}}$ $V a r [(\frac{X^{'} ϵ}{\sqrt{n}})] = {σ_{ϵ}}^{2} E [X^{'} X]$ Dado lo anterior ahora sabemos que $(\frac{X^{'} ϵ}{\sqrt{n}}) \sim N (0, {σ_{ϵ}}^{2} E [X^{'} X])$ Y volviendo a nuestra ecuación inicial $\sqrt{n} (\hat{β} - β) = \underset{E [X^{'} X]^{- 1}}{\underset{⏟}{(\frac{X^{'} X}{n})^{- 1}}} \underset{N (0, {σ_{ϵ}}^{2} E [X^{'} X])}{\underset{⏟}{(\frac{X^{'} ϵ}{\sqrt{n}})}}$ Y aqui es donde entra Slustky, ya que este teorema nos dice que Si $Z_{n} \underset{D i s t r i b u c i o n}{\underset{⏟}{⟶}} N (0, I)$ y $A_{n} \underset{p r o b a b i l i d a d}{\underset{⏟}{⟶}} A$ Entonces $Z_{n} A_{n} \underset{D i s t r i b u c i o n}{\underset{⏟}{⟶}} N (0, A \sum A^{'})$ En nuestro caso, $A = E [X^{'} X]^{- 1}$ Y $Z_{n} = (\frac{X^{'} ϵ}{\sqrt{n}}) \sim N (0, {σ_{ϵ}}^{2} E [X^{'} X])$ por lo que ya sabemos como terminar la demostración:

El valor esperado:
$E [A z_{n}] = A E [Z] = 0$ La varianza: $V a r [A Z_{n}] = A V a r (Z) A^{'}$ $V a r [A Z_{n}] = E [X^{'} X]^{- 1} V a r (Z) E [X^{'} X]^{- 1^{'}}$ Pero recordemos que $Z_{n} = (\frac{X^{'} ϵ}{\sqrt{n}}) \sim N (0, {σ_{ϵ}}^{2} E [X^{'} X])$ , por lo que conocemos cual es la varianza de $Z$ $V a r [A Z_{n}] = E [X^{'} X]^{- 1} {σ_{ϵ}}^{2} E [X^{'} X] E [X^{'} X]^{- 1^{'}}$ $V a r [A Z_{n}] = {σ_{ϵ}}^{2} E [X^{'} X] \underset{I}{\underset{⏟}{E [X^{'} X]^{- 1} E [X^{'} X]^{- 1^{'}}}}$ $V a r [A Z_{n}] = {σ_{ϵ}}^{2} E [X^{'} X] = {σ_{ϵ}}^{2} {\frac{(X^{'} X)}{n}}^{- 1}$ Finalmente, conocemos la distribución y los momentos muéstrales de $\sqrt{n} (β - \hat{β})$ $\sqrt{n} (β - \hat{β}) D ⟶ N (0, {σ_{ϵ}}^{2} {\frac{(X^{'} X)}{n}}^{- 1})$ Resumiendo, partimos del estimador de $\hat{β}$ para demostrar que cuando tenemos un n muy grande, sin importar como se distribuye el error, nuestro estimador $\hat{β}$ seguirá siendo útil para calcular nuestros estadísticos t y F\footnote{De hecho, siguiendo el mismo procedimiento se puede demostrar que $\hat{β}$ se distribuye normal con media $β$ y varianza ${σ_{ϵ}}^{2} (X^{'} X)^{- 1}$ . Sin el supuesto de normalidad, no conocíamos la distribución de $\hat{β}$ , y por ende, no podíamos construir la t. Al demostrar que $\sqrt{n} (β - \hat{β}) D ⟶ N (0, A V a r (\hat{β}))$ podemos construir la t y la F sin ningún problema.

Veamoslo en Stata:


clear
capture program drop  MCO
program define MCO, rclass
args N
clear
set obs `N'
capture drop y x
gen x=runiform(0,8)
gen y = 0.5*x+runiform(0,5)
qui reg y x
return scalar beta = _b[x]
end


simulate Beta1000=r(beta), reps(1000) nodots: MCO 1000
save Beta1000.dta
simulate  Beta10000=r(beta), reps(1000) nodots: MCO 10000
merge 1:1   _n using beta1000
kdensity Beta1000, n(500) generate(x_1000 f_1000) kernel(gaussian) nograph
label variable f_1000 "N=1000"
kdensity  Beta10000, n(500) generate(x_10000 f_10000) kernel(gaussian) nograph
label variable f_10000 "N=10000"
graph twoway (line f_1000 x_1000) (line f_10000 x_10000)

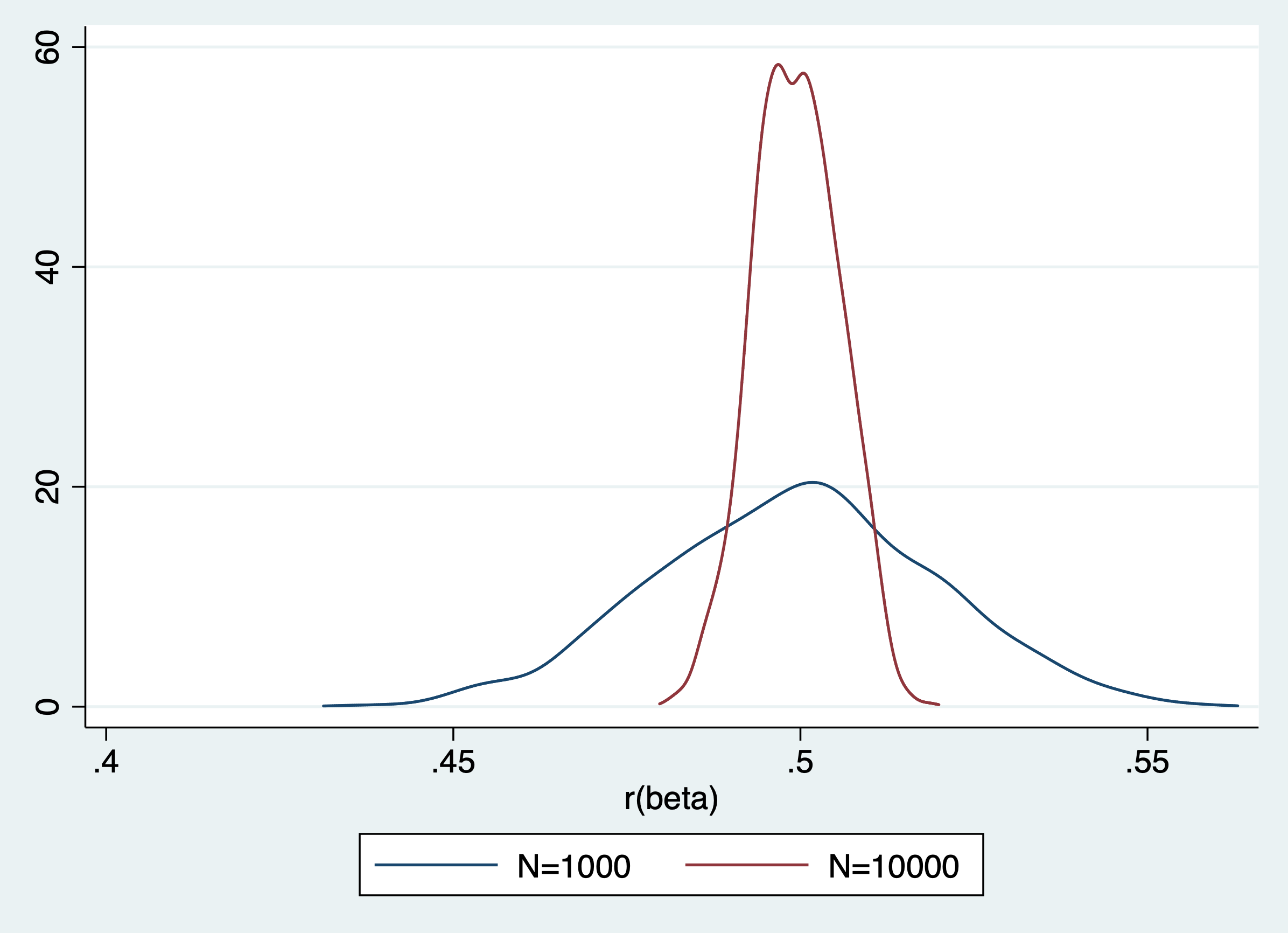
Como podemos ver nuestro estimador es consistente y a medida que aumenta la muestra, la probabilidad que la estimación se aleje del valor poblacional disminuye, pero como se había mencionado anteriormente esta el problema de que su distribución cambia a medida que cambia la muestra. La distribución del estimador con n = 10000 esta mucho mas concentrada.

Dado lo anterior optaremos por utilizar una version de los estimadores recentrados y escalados.


replace  Beta1000=sqrt(1000)*(Beta1000-0.5)
replace  Beta10000=sqrt(10000)*(Beta10000-0.5)
drop x_1000 f_1000 x_10000 f_10000
kdensity Beta1000, n(500) generate(x_1000 f_1000) kernel(gaussian) nograph
label variable f_1000 "N=1000"
kdensity Beta10000, n(500) generate(x_10000 f_10000) kernel(gaussian) nograph
label variable f_10000 "N=10000"
graph twoway (line f_1000 x_1000) (line f_10000 x_10000) (function normalden(x, sqrt(0.5)),range(-2 2)) , legend(label(3 "Distribución Normal"  cols(3))

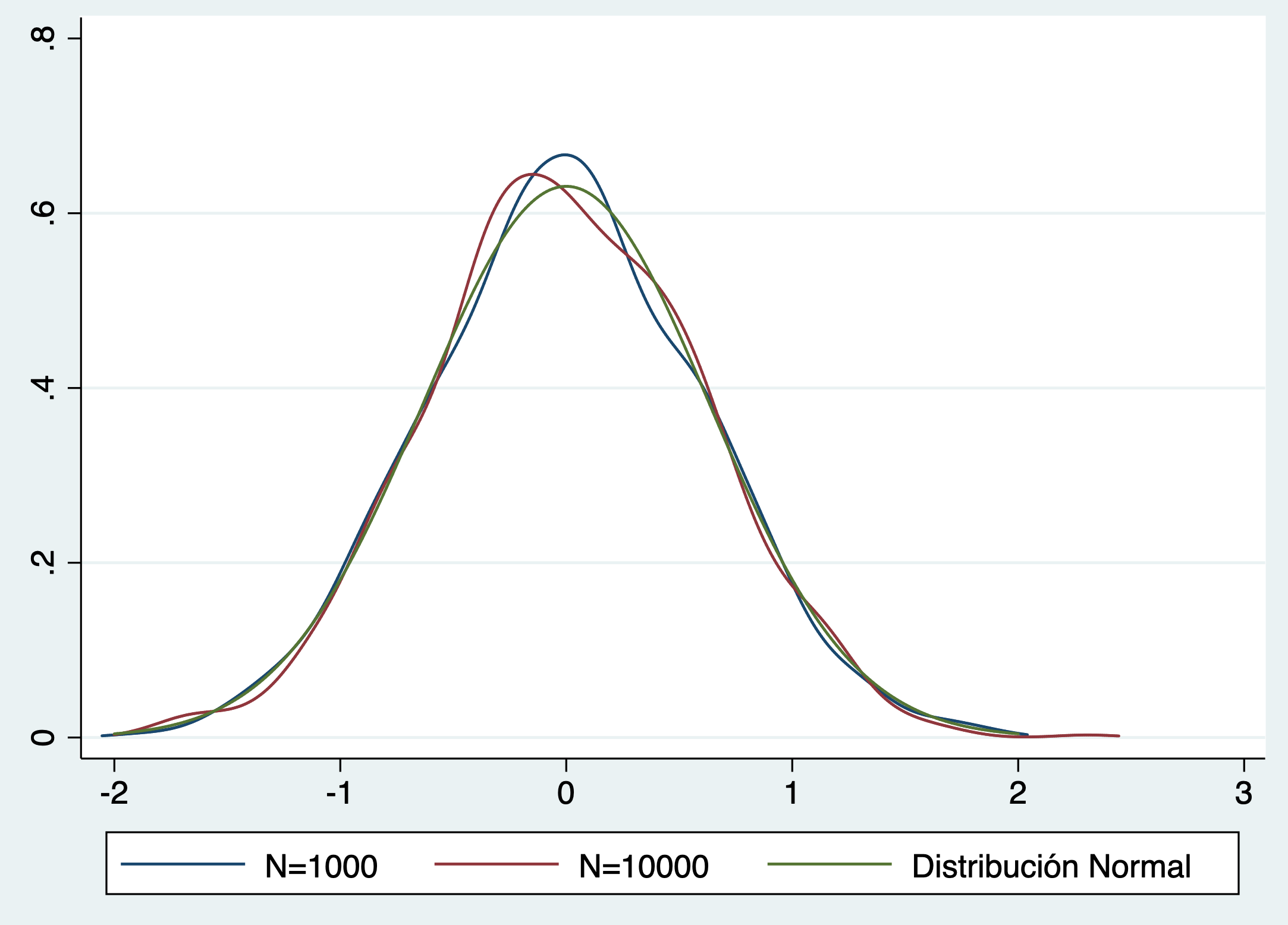
En esta ultima grafica vemos como los estimadores recentrados y escalados tienen una distribución prácticamente igual a la de una normal independiente del N. Ahora si podemos usar nuestros estadísticos f y t y hacer inferencia sin problema.

Bibliografía:

Verbeek, M. (2004), A Guide to Modern Econometrics.
Drukker, D. (2017), Consistencia y Normalidad Asintótica: Una Explicación con Simulaciones.
Wooldridge, Jeffrey M. (2018), Introductory Econometrics: A Modern Approach, Sixth Edition, Cengage Learning.
Montenegro, A. (2018), Econometría Intermedia y Básica.

Supuesto: 3
Normalidad