Exogeneidad Estricta
El supuesto de exogeneidad estricta hace referencia a que los errores no pueden estar correlacionados con ninguno de nuestros regresores, es decir: $$ E[\epsilon|X] = 0 $$ En esta parte veremos cuando se viola este supuesto, y su posible solución. Tenemos 3 casos en los que hay problemas de endogeneidad. Estos casos son: 1. Omisión de variables relevantes, 2. Errores de medición, y 3. Simultaneidad.
Omisión de variables relevantes
Supongamos que el modelo correcto es el siguiente: $$ y = X_{r}\beta_{r} + X_{s}\beta_{s} + \mu $$ Pero por alguna razón nosotros estimamos: $$ y = X_{r}\beta_{r} + \epsilon $$ Intuitivamente sabemos que esto nos va a generar un sesgo en nuestro estimador (sesgo por variable omitida). Veamos porque: $$ \hat{\beta_{r}} = (X_{r}'X_{r})^{-1}X_{r}'y $$ Al remplazar por $y$ del modelo correcto y algo de matemáticas $$ \hat{\beta_{r}} = (X_{r}'X_{r})^{-1}X_{r}'(X_{r}\beta_{r} + X_{s}\beta_{s} + \mu) $$ $$ \hat{\beta_{r}} = (X_{r}'X_{r})^{-1}X_{r}'X_{r}\beta_{r} + (X_{r}'X_{r})^{-1}X_{r}'X_{s}\beta_{s} + (X_{r}'X_{r})^{-1}X_{r}'\mu $$ $$ \hat{\beta_{r}} = \beta_{r} + (X_{r}'X_{r})^{-1}X_{r}'X_{s}\beta_{s} + (X_{r}'X_{r})^{-1}X_{r}'\mu $$ Sacando valor esperado $$ E[\hat{\beta_{r}}] = \beta_{r} + E[(X_{r}'X_{r})^{-1}X_{r}'X_{s}\beta_{s}] + E\cancelto{0}{[(X_{r}'X_{r})^{-1}X_{r}'\mu]} $$ $$ E[\hat{\beta_{r}}] = \beta_{r} + \underbrace{E[(X_{r}'X_{r})^{-1}X_{r}'X_{s}\beta_{s}]}_{Sesgo} $$ Como vemos, al omitir una variable importante, se nos esta generando un sesgo. La pregunta ahora es ¿Cual es la dirección de este sesgo?. Esto depende de dos cosas, primero del signo de $\beta_{s}$ y segundo del signo de la $cov(X_{r}, X_{s})$.
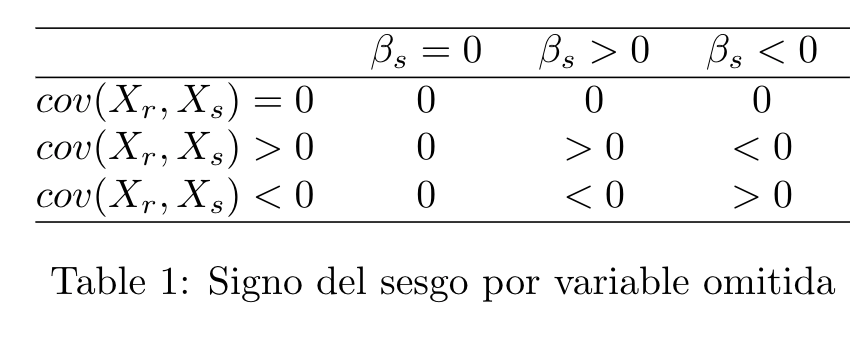
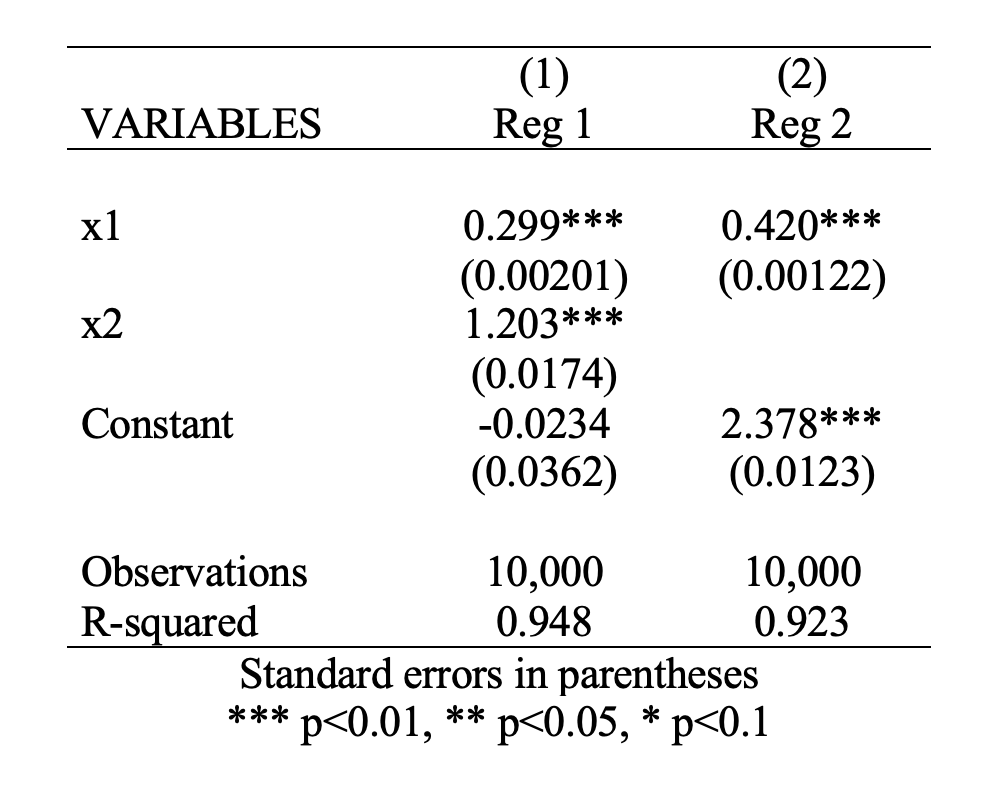
Para aterrizar un poco más este concepto, imaginemos que estamos tratando de estimar el salario de las personas. Omitimos habilidad ya que no contamos con una forma de medirla, y estimamos el parámetro para años de educación $\beta_{educ}$. Para saber cual sera el sesgo debemos pensar en dos cosas. Primero, es posible que $\beta_{habilidad} > 0$, es decir, que la habilidad afecte positivamente al salario, y segundo también tiene sentido pensar que existe una relación positiva entre años de educación y habilidad (se podría argumentar que entre mas hábil soy, soy mas propenso a estudiar ya que se me facilita mas), por lo que $cov(Educacion,Habilidad) > 0$. Si vemos en la tabla, veremos entonces que nuestro estimador para $\beta_{educ}$ tendra un sesgo positivo. Otra pregunta interesante es si este sesgo se soluciona cuando n tiende a infinito. Para ver esto, tomaremos nuestro estimador sesgado $\beta_{r}$ (antes de sacarle valor esperado) y le aplicaremos $plim$. $$ plim[\hat{\beta_{r}}] = plim[\beta_{r} + (X_{r}'X_{r})^{-1}X_{r}'X_{s}\beta_{s} + (X_{r}'X_{r})^{-1}X_{r}'\mu (\frac{n}{n})] $$ $$ plim[\hat{\beta_{r}}] = plim[\hat{\beta_{r}} (\frac{n}{n})] + plim[(\frac{X_{r}'X_{r}}{n})^{-1} (\frac{X_{r}'X_{s}}{n}) \beta_{s}] + plim[(\frac{X_{r}'X_{r}}{n})^{-1} (\frac{X_{r}'\mu}{n})] $$ $$ plim[\hat{\beta_{r}}] = \beta_{r} + \underbrace{E[X'X]^{-1}E[X_{r}'x_{s}]\beta_{s}}_{Inconsistente} $$ Asi que como acabamos de ver cuando omitimos una variable importante en nuestra regresion, vamos a tener estimadores sesgados e inconsistentes. Un dato a tener en cuenta es que estos estimadores sesgados tendrán una varianza menor a los estimadores correctos simplemente por el hecho de tener menos variables. $$ Var[\widetilde{\beta_{r}}] = {\sigma_{\epsilon}^{2}} (X_{r}'X_{r})^{-1} $$ $$ Var[\hat{\beta_{r}}] = {\sigma_{\epsilon}^{2}} \frac{(X_{r}'X_{r})^{-1}}{1 - {R^{2}_{Xr,Xs}}} $$ $$ Var[\widetilde{\beta_{r}}] < Var[\hat{\beta_{r}}] $$
clear
set obs 10000
gen x1=rnormal(1,10)
gen x2= 0.1*x1 + runiform(1,3)
gen epsilon =rnormal()
gen y= 0.3*x1 + 1.2*x2 + epsilon

reg y x1 x2
outreg2 using reg1.doc, replace ctitle(Reg 1)
reg y x1
outreg2 using reg1.doc, append ctitle(Reg 2)
Error de medición
Por otra parte, los errores de medición también nos causan problemas en nuestros estimadores. Como vamos a ver, hay dos tipos de errores de medición; en $y$ y en $x$, es decir, en nuestra variable dependiente y en nuestras variables independientes. Como veremos mas adelante, los errores de medición en $y$ no nos generan problemas de sesgo ni de consistencia, pero si en eficiencia. Por otra parte, errores de medición en $x$ si nos van a generar un sesgo, llamado el sesgo de atenuación.Errores de medición en y:
Supongamos que al medir nuestra variable dependiente, obtenemos el dato verdadero de $y$ mas un sesgo $w$. Adicional a esto, sabemos que este error $w \sim iid(0,{\sigma_{w}}^{2})$. $$y^{*} = y + w$$ Adicional a lo anterior, sabemos también este error no esta correlacionado con ni con el error ni con ninguna otra variable explicativa, es decir: $$cov(w,\epsilon) = 0$$ $$cov(w,x) = 0$$ Dado esta información miremos primero que pasa con nuestros estimadores. $$\hat{\beta} = (X'X)^{-1}X'y$$ Nosotros creemos que estamos realizando la regresión contra $y$, pero en realidad nosotros tenemos $y^{*}$, por lo que estamos haciendo la regresion en $y = y^{*} - w$ (Acá solo despeje $y$ de la ecuación de arriba). Remplazando esto tenemos que: $$\hat{\beta} = (X'X)^{-1}X'(y^{*} - w)$$ $\hat{\beta} = (X'X)^{-1}X'(X\beta + \epsilon - w)$ $$\hat{\beta} = \beta + (X'X)^{-1}X' \epsilon - (X'X)^{-1}X'w $$ Sacando valor esperado $$E[\hat{\beta}] = \beta + \cancelto{0}{E[(X'X)^{-1}X' \epsilon}] - \cancelto{0}{E[(X'X)^{-1}X'w]}$$ Podemos cancelar el tercer termino, $E[(X'X)^{-1}X'w]$, ya que al iniciar dijimos que $cov(X,w) = 0$. En otras palabras, a pesar del problema de error en la medicion de $y$, podemos seguir obteniendo estimadores insesgados pero solo cuando el error $w$ no esta relacionado con ninguno de los regresores. Ahora miremos que pasa cuando sacamos el $plim$ $$\hat{\beta} = (X'X)^{-1}X'(y^{*} - w)$$ Multiplicando por $\frac{n}{n}$ $$\hat{\beta} = {(\frac{X'X}{n})}^{-1} (\frac{X'(X\beta + \epsilon - w)}{n})$$ $$\hat{\beta} = {(\frac{X'X}{n})}^{-1} {(\frac{X'X}{n})}\beta + {(\frac{X'X}{n})}^{-1} (\frac{X' \epsilon}{n}) - {(\frac{X'X}{n})}^{-1} (\frac{X' w}{n})$$ $$plim[\hat{\beta}] = \beta + plim{(\frac{X'X}{n})}^{-1} plim(\frac{X' \epsilon}{n}) - plim{(\frac{X'X}{n})}^{-1} plim(\frac{X' w}{n})$$ $$plim[\hat{\beta}] = \beta + E[X'X]^{-1} E[X' \epsilon] - E[X'X]^{-1} E[X'w]$$ Pero si se cumple que $E[X' \epsilon] = 0$ y $E[X'w] = 0$, entonces: $$plim[\hat{\beta}] = \beta + E[X'X]^{-1} \cancelto{0}{E[X' \epsilon]} - E[X'X]^{-1} \cancelto{0}{E[X'w]}$$ $$plim[\hat{\beta}] = \beta$$ Nuestros estimadores son consistentes. Acabamos de ver entonces que a pesar de tener errores en la medición de $y$, nuestro estimador $\hat{\beta}$ es insesgado y consistente. Ahora solo nos falta ver que pasa con la varianza: $$Var[\hat{\beta}] = Var[\beta + (X'X)^{-1}X' \epsilon - (X'X)^{-1}X'w ]$$ $$Var[\hat{\beta}] = 0 + (X'X)^{-1}X'Var[\epsilon]X(X'X)^{-1} + (X'X)^{-1}X'Var[w]X(X'X)^{-1} - \cancelto{0}{2cov(\epsilon,w)}$$ Suponiendo homocedasticidad $$Var[\hat{\beta}] = 0 + (X'X)^{-1}X'{\sigma_{\epsilon}}^{2}X(X'X)^{-1} + (X'X)^{-1}X'{\sigma_{w}}^{2}X(X'X)^{-1}$$ $$Var[\hat{\beta}] = {\sigma_{\epsilon}}^{2}\underbrace{(X'X)^{-1}X'X}_{I}(X'X)^{-1} + {\sigma_{w}}^{2}\underbrace{(X'X)^{-1}X'X}_{I}(X'X)^{-1}$$ $$Var[\hat{\beta}] = ({\sigma_{\epsilon}}^{2} + {\sigma_{w}}^{2})(X'X)^{-1}$$ Como podemos ver, nuestra varianza de MCO pierde eficiencia al tener problemas de medición sobre $y$. Para concluir esta primera parte de problemas de medición, vemos que cuando el problema esta en la variable dependiente, tendremos estimadores insesgados, consistentes pero perderemos eficiencia, es decir, tendremos una varianza alta.Errores de medición en x:
Ahora veamos el caso en el que nuestros errores de medicion estan en x. Supongamos que nosotros observamos $$x^{*} = x + w$$ Por lo que ahora tendremos $$y = (X + w)\beta + \epsilon$$ $$y = X\beta + \underbrace{\epsilon + w\beta}_{Nuevo - Error}$$ Entonces con los datos que tenemos, calculamos nuestro estimador: $$\hat{\beta} = (X'X)^{-1}X'y$$ $$\hat{\beta} = (X'X)^{-1}X'(X\beta + {\epsilon + w\beta})$$ $$\hat{\beta} = \underbrace{(X'X)^{-1}X'X}_{I}\beta + (X'X)^{-1}X'\epsilon + (X'X)^{-1}X'w\beta$$ $$\hat{\beta} = \beta + (X'X)^{-1}X'\epsilon + (X'X)^{-1}X'w\beta$$ Sacando valor esperado: $$\hat{\beta} = \beta + \cancelto{0}{E[(X'X)^{-1}X'\epsilon]} + E[(X'X)^{-1}X'w\beta]$$ $$\hat{\beta} = \beta + \underbrace{E[(X'X)^{-1}X'w\beta]}_{Sesgo}$$ Este sesgo puede ser escrito de otra forma: $$\hat{\beta} = \beta + E[(X'X)^{-1}] E[X'w]\beta$$ Remplazando $X'$ por $(X^{*} - w)'$ $$\hat{\beta} = \beta + E[(X'X)^{-1}] E[(X^{*} - w)'w]\beta$$ $$\hat{\beta} = \beta + E[(X'X)^{-1}] E[X^{*'}w - w'w]\beta$$ $$E[\hat{\beta}] = \beta + E[(X'X)^{-1}] \cancelto{0}{E[X^{*'}w]\beta} - E[(X'X)^{-1}]E[w'w]\beta$$ $$E[\hat{\beta}] = \beta - E[(X'X)^{-1}]E[w'w]\beta$$ $$E[\hat{\beta}] = \beta - \underbrace{E[(X'X)^{-1}]}_{Var(X)^{-1}}\underbrace{E[w'w]}_{Var(w)}\beta$$ $$E[\hat{\beta}] = \beta - Var(X)^{-1}Var(w)\beta$$ Pero $Var(X) = Var(x^{*} - w)$ $$E[\hat{\beta}] = \beta(1 - \frac{{\sigma_{w}}^{2}}{{\sigma_{X^{*}}}^{2} + {\sigma_{w}}^{2}})$$ $$E[\hat{\beta}] = \beta\underbrace{[\frac{{\sigma_{X}}^{*2}}{{\sigma_{X^{*}}}^{2} + {\sigma_{w}}^{2}} ]}_{S. Atenuacion}$$ Como podemos ver, problemas en la medición de $x$ nos traen problemas de sesgo en nuestros estimadores. Aparece este problema llamado \textbf{sesgo de atenuación} el cual esta siempre entre 0 y 1 por lo que $\hat{\beta} < \beta$, es decir, nuestros estimadores van a sub estimar siempre al parámetro poblacional. Ahora preguntémonos que pasa con la varianza de $\hat{\beta}$ cuando hay error de medición en x, partiendo de: $$\hat{\beta} = \beta + (X'X)^{-1}X'\epsilon + (X'X)^{-1}X'w\beta$$ $$Var[\hat{\beta}] = 0 + Var[(X'X)^{-1}X'\epsilon] + Var[(X'X)^{-1}X'w\beta] + \cancelto{0}{2Cov(\epsilon, w\beta)} $$ $$Var[\hat{\beta}] = (X'X)^{-1}X'Var[\epsilon]X(X'X)^{-1} + (X'X)^{-1}X'Var[w\beta]X(X'X)^{-1} $$ $$Var[\hat{\beta}] = {\sigma_{\epsilon}}^{2}(X'X)^{-1}\underbrace{X'X(X'X)^{-1}}_{I} + {\beta}^{2}{\sigma_{w}}^{2}(X'X)^{-1}\underbrace{X'X(X'X)^{-1}}_{I} $$ $$Var[\hat{\beta}] = ({\sigma_{\epsilon}}^{2} + {\beta}^{2}{\sigma_{w}}^{2} )(X'X)^{-1}$$ Vemos un resultado muy similar al punto anterior (cuando el error de medición estaba en $y$), por lo que para concluir podemos decir que cuando hay errores de medición en x, además de tener estimadores sesgados, también pierden eficiencia.
PENDIENTE

Simultaneidad
Llegamos al ultimo caso, que nos genera problemas de endogeneidad. Esto es, cuando hay simultaneidad. Para explicar esto, veamos el siguiente caso: Queremos investigar si un mayor numero de policías disminuye el crimen en las regiones, hacemos una regresión con los datos que tenemos sobre tasa de crimen y numero de policías y encontramos que los lugares con mas policías tienen mas crimen. ¿Por qué? ¿Sera que los policías están cometiendo crímenes?, en teoría esto no tiene mucho sentido. Lo que puede estar pasando es que evidentemente si una región tiene muchos policías es porque ahí hay una tasa de crimen muy alta, y el estado envió muchos policías a que controlen el crimen. Entonces el problema al que nos enfrentamos en este tipo de casos es el siguiente: $$Homicidios_{t} = \beta_{0} + \beta_{1}Policia_{t} + \epsilon_{1}$$ $$Policia_{t} = \alpha_{0} + \alpha_{1}Homicidios_{t} + \epsilon_{2}$$ Como vemos en las dos ecuaciones anteriores, cada variable esta explicada parcialmente \footnote{Digo parcialmente porque hay mas variables que afectan la cantidad de policías en una región o los homicidios.} por la otra. Intuitivamente podemos decir que cuando hay mas policías, se esperaría que los homicidios disminuyeran ya que la probabilidad de ser capturado aumenta, y esto desincentiva los crímenes, pero por otra parte, cuando hay mas homicidios se esperaría también que los policías aumenten en respuesta a este aumento en el crimen. Cuando vamos a investigar esta relación entre homicidios y numero de policías podemos entrar en el problema de que no sabemos que variable esta explicando que. Es decir, no sabemos si nuestros datos nos están explicando la ecuación de $homicidios(x_{1},x_{2},...,policias, x_{k})$ o $policias(x_{1},x_{2},...,homicidios, x_{k})$. Veamos matemáticamente que en la regresión hipotética que propusimos al inicio, estamos encontrando que mas policías aumentan los homicidios. Sustituyendo la ecuación de policías en homicidios obtenemos que: $$Homicidios_{t} = \beta_{0} + \beta_{1}[\alpha_{0} + \alpha_{1}Homicidios_{t} + \epsilon_{1}] + \epsilon_{2}$$ $$ Homicidios_{t} = \beta_{0} + \beta_{1}\alpha_{0} + \beta_{1}\alpha_{1}Homicidios_{t} + \beta_{1}\epsilon_{1} + \epsilon_{2}$$ $$ Homicidios_{t}( 1 - \beta_{1}\alpha_{1})= \beta_{0} + \beta_{1}\alpha_{0} + \beta_{1}\epsilon_{1} + \epsilon_{2}$$ $$ Homicidios_{t}= \frac{\beta_{0} + \beta_{1}\alpha_{0}}{( 1 - \beta_{1}\alpha_{1})} + \frac{\beta_{1}\epsilon_{1} + \epsilon_{2}}{( 1 - \beta_{1}\alpha_{1})}$$ Como podemos ver, homicidios esta siendo afectado por muchos parámetros que no estábamos teniendo en cuenta. Esto se debe a que la correlación entre policías y el error $\epsilon_{1}$ no es 0. Si hacemos lo mismo para policías obtendremos que: $$Policia = \frac{\alpha_{0} + \alpha_{1}\beta_{0}}{1 - \alpha_{1}\beta_{1}} + \frac{\alpha_{1}\epsilon_{1} + \epsilon_{2}}{1 - \alpha_{1}\beta_{1}}$$ Y con este ultimo resultado podemos ver porque la correlacion entre policias y el error es diferente de 0: $$Cov(Policia,\epsilon_{1}) = E[Policia*\epsilon_{1}] + E[Policia]*\cancelto{0}{E[\epsilon_{1}]}$$ $$Cov(Policia,\epsilon_{1}) = E[Policia*\epsilon_{1}]$$ $$Cov(Policia,\epsilon_{1}) = E[(\frac{\alpha_{0} + \alpha_{1}\beta_{0}}{1 - \alpha_{1}\beta_{1}} + \frac{\alpha_{1}\epsilon_{1} + \epsilon_{2}}{1 - \alpha_{1}\beta_{1}})\epsilon_{1}]$$ $$Cov(Policia,\epsilon_{1}) = E[(\frac{\alpha_{0} + \alpha_{1}\beta_{0}}{1 - \alpha_{1}\beta_{1}})\epsilon_{1} + (\frac{\alpha_{1}\epsilon_{1} + \epsilon_{2}}{1 - \alpha_{1}\beta_{1}})\epsilon_{1}]$$ $$Cov(Policia,\epsilon_{1}) = \cancelto{0}{E[(\frac{\alpha_{0} + \alpha_{1}\beta_{0}}{1 - \alpha_{1}\beta_{1}})\epsilon_{1}]} + E[(\frac{\alpha_{1}\epsilon_{1}} {1 - \alpha_{1}\beta_{1}})\epsilon_{1}] + \cancelto{0}{E[(\frac{\epsilon_{2}} {1 - \alpha_{1}\beta_{1}})\epsilon_{1}]} $$ $$Cov(Policia,\epsilon_{1}) = E[(\frac{\alpha_{1}{\epsilon_{1}}^{2}} {1 - \alpha_{1}\beta_{1}})] = \frac{\alpha_{1}{\sigma_{\epsilon}}^{2}}{1 - \alpha_{1}\beta_{1}}\not= 0 $$ Usando toda la información que obtuvimos anteriormente vamos ahora a buscar cual es el sesgo que nos genera tener problemas de simultaneidad. Partiendo de nuestro estimador de MCO: $$\hat{\beta} = (X'X)X'y$$ Y poniéndolo en términos de las variables del ejemplo anterior: $$\hat{\beta} = (Policia'Policia)^{-1}Policia'Homicidios $$ $$ \hat{\beta} = (Policia'Policia)^{-1}Policia'(Policia\beta + \epsilon_{1})$$ $$ \hat{\beta} = \underbrace{(Policia'Policia)^{-1}Policia'Policia}_{I}\beta + (Policia'Policia)^{-1}Policia'\epsilon_{1}$$ $$ \hat{\beta} = \beta + (Policia'Policia)^{-1}Policia'\epsilon_{1}$$ Ahora antes de continuar, pensemos en el segundo termino de la ecuación anterior. ¿A que se parece?. Tiene la misma forma que tendría una regresión de $\epsilon$ en $Policia$. Es decir, este ultimo termino es el $\hat{\pi}_{Policia}$\footnote{Escribo $\hat{\pi}$ para que quede claro que es una estimación totalmente diferente a la que veníamos haciendo, pero que sigue siendo un parámetro estimado por MCO.} de la regresión $\epsilon = \rho_{0} + \rho_{1}Policia + z$. $$ \hat{\beta} = \beta + \underbrace{(Policia'Policia)^{-1}Policia'\epsilon_{1}}_{\hat{\pi}}$$ $$\hat{\pi} = (Policia'Policia)^{-1}Policia'\epsilon_{1} = \frac{Cov(Policia,\epsilon_{1})}{Var(Policia)}$$ ¿Porque estoy escribiendo la covarianza de policía y Epsilon 1 sobre la varianza de policía? Porque este es el estimador $\hat{\beta}$ escrito en forma de sumatorias\footnote{Recordemos el estimador de MCO en notación de sumatorias: $\hat{\beta} = \frac{\sum (x_{i} - \bar{x})(y_{i} - \bar{y})}{\sum (x_{i} - \bar{x})^{2}} = \frac{Cov(x,y)}{Var(x)}$.}. Entonces volviendo a donde estábamos, podemos escribir $\hat{\beta}$ de la siguiente forma: $$ \hat{\beta} = \beta + \frac{Cov(Policia,\epsilon_{1})}{Var(Policia)} $$ Y usando nuestro resultado anterior sobre la covarianza de policía y epsilon 1: $$ \hat{\beta} = \beta + \frac{\frac{\alpha_{1}{\sigma_{\epsilon}}^{2}}{1 - \alpha_{1}\beta_{1}}}{{\sigma^{2}_{policia}}} $$ $$\hat{\beta} = \beta + \underbrace{\frac{\alpha_{1} {\sigma_{\epsilon}}^{2} }{(1 - \alpha_{1}\beta_{1}){\sigma^{2}}_{policia}} }_{S. Simultaneidad}$$ Acabamos de demostrar que nuestros estimadores de MCO de la regresión de Homicidios en policías tiene un sesgo. Intuitivamente ya lo sabíamos, pero ahora conocemos la forma exacta. Pensemos ahora que dirección tiene este sesgo de simultaneidad: $$Sesgo = \frac{\alpha_{1} {\sigma_{\epsilon}}^{2} }{(1 - \alpha_{1}\beta_{1}){\sigma^{2}}_{policia}} $$ Por una parte, las varianzas son siempre positivas. Asi que la direccion del sesgo depende del signo de $\alpha_{1}$ y de $\beta_{1}$. Para nuestro ejemplo de cantidad de policias y homicidios, $\alpha_{1}$ es igual al efecto de los homicidios en la cantidad de policias. Intuitivamente podemos decir que esto es positivo, ya que entre mas homicidios hay en una region, mas policias seran enviados a controlar el problema. Por otro lado, $\beta_{1}$ podria tener un signo negativo, ya que se puede pensar que ante un aumento de policias en una determinada region, los homicidios van a disminuir. Dicho esto tenemos que $\alpha_{1} > 0$ y que $\beta_{1} < 0$, por lo que nuestro sesgo de simultaneidad sera positivo. $$Sesgo = \frac{\overbrace{\alpha_{1} {\sigma_{\epsilon}}^{2}}^{Positivo} }{\underbrace{(1 - \alpha_{1}\beta_{1})}_{Positivo}\underbrace{{\sigma^{2}}_{policia}}_{Positivo}} $$ $$Sesgo > 0$$ Dado esto acabamos de mostrar que este problema de simultaneidad también nos afecta nuestros estimadores, haciéndolos sesgados. Lo que sigue ahora es buscar soluciones a nuestros problemas de endogeneidad. Aparecen entonces dos posibles soluciones. Por ejemplo para solucionar nuestro problema de simultaneidad podemos utilizar utilizar variables rezagadas, es decir, usar variables en diferentes periodos de tiempo para ver por ejemplo, si una mayor cantidad de policias ayer, se traduce en una menor tasa de crimen hoy. La otra solución es un poco mas "interesante", ya que con esta podemos solucionar cualquiera de los tres problemas mencionados anteriormente. Sin importar si tenemos variables omitidas, errores de medición o simultaneidad, el método de variables instrumentales nos sirve para estimar nuestros parámetros sin problema.
PENDIENTE

Bibliografía:
- Díaz, A. (2020), Clases Econometría Avanzada.
- Verbeek, M. (2004), A Guide to Modern Econometrics.
- Wooldridge, Jeffrey M. (2018), Introductory Econometrics: A Modern Approach, Sixth Edition, Cengage Learning.
- Montenegro, A. (2018), Econometría Intermedia y Básica.